Applications of the Option Pricing
Paradigm to Insurance
by
Michael Wacek
Discussion by
Stephen Mildenhall
CNA Re, Chicago IL
Contents
What is Black Scholes?
Black Scholes is a mathematical theorem: a statement that certain
conclusions follow from certain premises
- Determines price of European call option on a stock
- Call Option is the right, but not obligation, to buy at a pre-determined
exercise or strike price
- European: can only be exercised at expiration
Assumptions
- Stock price:
- Follows a "geometric Brownian motion"
- Instantaneous
stock returns are normally distributed
- No stock dividends are payable during life of the derivative
- Continuous time trading
- Infinitely divisible securities (e.g. can buy 0.1234 a stock)
- Ability to borrow and lend at a fixed risk free rate of interest
r
- r is fixed regardless of duration
- No restrictions on short selling; full use of proceeds
- No transaction costs or taxes
- No arbitrages
- Whether Black Scholes is true in the "real world"
depends on whether the premises hold in the real world
Black Scholes is very complete pricing Paradigm
- Gives price and an explicit way to "hedge" (manufacture)
the product for the indicated price by trading in the underlying stock and
bonds
- Like an insurance pricing model plus a reinsurance structure
guaranteeing results!
- Regardless of state of reinsurance market
Black Scholes Pricing and Market Pricing
|
Ex Price
|
Intrinsic
Value
|
Market
Price
|
BS
|
Pct Error
|
Actuarial
|
Volume
|
|
750
|
169.77 |
186 |
181.06
|
-2.7% |
201.99
|
714 |
|
805
|
114.77 |
135 |
130.90
|
-3.0% |
150.55
|
3 |
|
890
|
29.77 |
67 1/2 |
66.90
|
-0.9% |
82.04
|
10 |
|
900
|
19.77 |
64 |
60.88
|
-4.9% |
75.32
|
6 |
|
910
|
9.77 |
59 1/4 |
55.22
|
-6.8% |
68.93
|
102 |
|
930
|
0 |
44 1/4 |
44.96
|
1.6% |
57.18
|
3,291 |
|
935
|
0 |
41 3/4 |
42.62
|
2.1% |
54.46
|
5 |
|
940
|
0 |
42 1/2 |
40.37
|
-5.0% |
51.83
|
264 |
|
950
|
0 |
36 1/4 |
36.12
|
-0.4% |
46.83
|
14 |
|
960
|
0 |
31 1/2 |
32.20
|
2.2% |
42.17
|
2 |
|
990
|
0 |
21 |
22.37
|
6.5% |
30.20
|
5 |
|
995
|
0 |
20 |
20.99
|
4.9% |
28.48
|
107 |
|
1025
|
0 |
11 |
14.07
|
27.9% |
19.71
|
7 |
|
|
|
|
|
|
|
- S&P 500 European Calls September 15, 1997
- S&P closed at 919.77
- Risk free rate of interest 5.12%, discount factor 0.9868
- 95 days to expiration
- Actuarial pricing assumes growth rate on stocks 15%
pa (13.98% compounded continuously) discounted at risk free rate
- Standard Deviation of stock returns: 23.5% annually
- Errors +/-7% over a large range except for one, very
out of the money call
- Last trade on may have been well before close
- Oh, for such a good way to price GL!
Insurance Interpretations
Aggregate Stop Loss Likened Call Option
- Agg stop "attaches" at a certain loss ratio
and pays the excess of actual losses over the attachment
- Agg stop with a limit = difference of two agg stops
with different attachments
- Call option has an "exercise" price and pays
the excess of the final stock price over the exercise price
- Ignore niceties of time and payout patterns: assume
agg stop settles in full T years from now with a single payment
- Could argue that agg stops are more like swaps than options
How do you price an Aggregate Stop Loss?
- S = aggregate loss random variable
- Current best estimate of losses at
expiration, T years from now
- k = attachment point
- Pure Premium = E[ max(S-k, 0) ]
- PV Pure Premium = e-r'TE[ max(S-k, 0) ] for some
discount rate r' per year
- Premium = ???
- Example
- S ~ Lognormal(m, s)
- Mean of log(S) is m and standard
deviation is s
- Selected discounting interest rate r'
- Discounted pure premium can be determined using Part 1 calculus
em+s2/2-r'T
F((ln(1/k)+(m+s2))/s) - e-r¢Tk F((ln(1/k)+m)/s)
- See appendix for details
- F is the cumulative distribution function of the standard normal distribution
An Actuarial Call Option Price
Black Scholes assumes stock prices follow a Geometric Brownian
Motion
- Changes in stock prices over a short period of time are approximately
normally distributed
- DS / S = mDt + sZÖDt, where Z is a standard normal random variable
- Mean return in small time period Dt is mDt
- Variance is s2Dt
- Is this reasonable? Below is a normal probability plot for
Dell stock daily returns 1/2/97 to 2/9/00
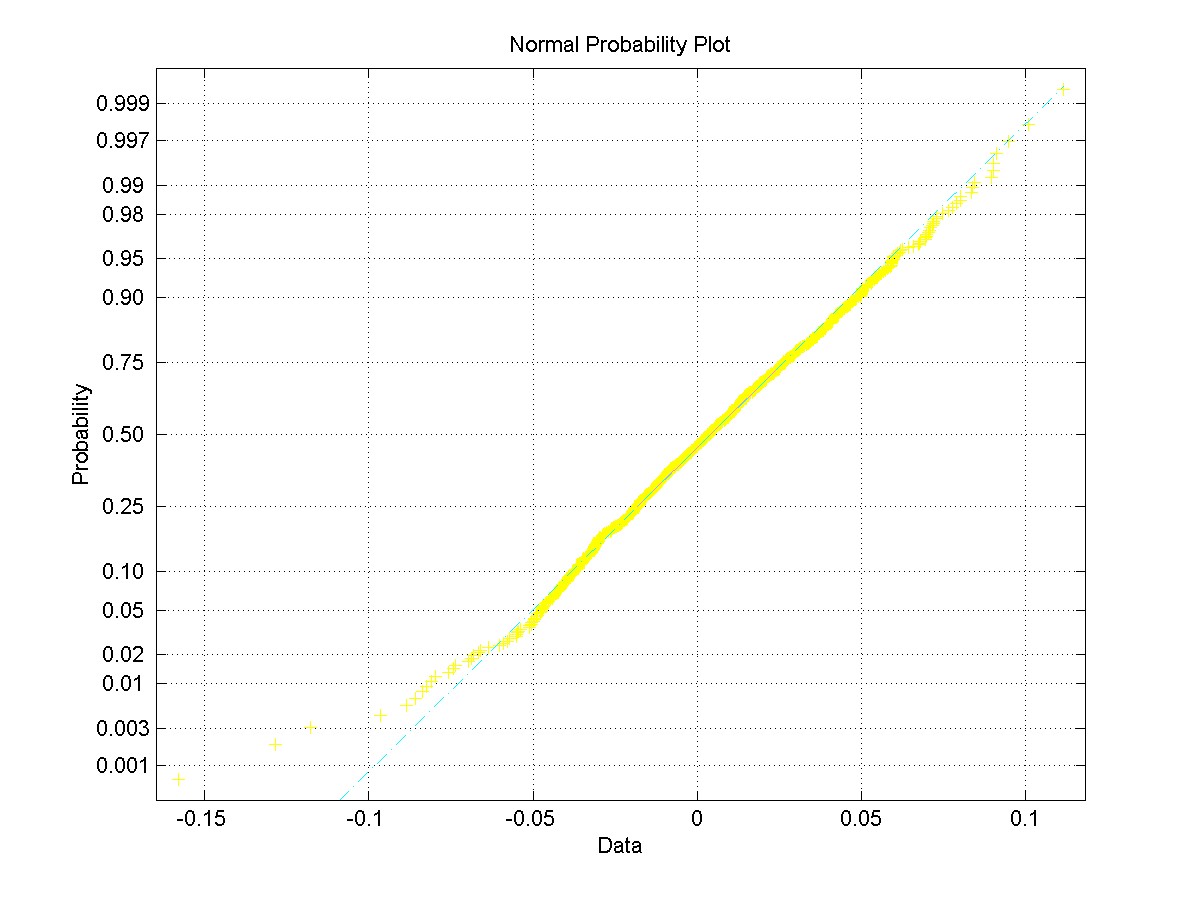
- Note problems with fit in extreme left tail
- Indicates trouble with assumptions for deeply in and
out of the money options (volatility smile)
- GBM implies that T years from now the stock price ST
is lognormal and
ln(ST/S0) ~ N((m-s2/2)T,
sT1/2)
Estimating Parameters
- Mean m: CAPM, historical record
- Standard deviation s: Historical
record, last thirty days returns.
- Finance has the data of an actuary's dreams!
- Discounting Interest Rate r': COTOR Comprehensive
Study, Zen Enlightenment
- Can now apply our agg stop pricing formula:
- e-r'TE[ max(ST-k, 0) ] = e-r'T
S0 E[ max(ST/S0 - k/S0, 0) ]
- m ¬ (m-s2/2)T
- k ¬ k/S0
- s ¬ sÖT
e(m-r¢) T S0 F(ln(S0/k)+(m+s2/2)T/sÖT) - e-r¢T k F(ln(S0/k)+(m-s2/2)T/sÖT)
- This formula appeared in a Samuelson paper published in the
1960's following the same logic used here
- Still issue of converting from discounted pure
premium to premium
- Actuarial Price in table assumes r=r' in above formula
Why Black Scholes is Surprising
Compare Black Scholes result with formula above
| Act: |
e(m-r¢) T
|
S0 F(ln(S0/k)+(m+s2/2)T/sÖT)
|
- |
e-r¢T k F(ln(S0/k)+(m-s2/2)T/sÖT) |
| BS: |
|
S0 F(ln(S0/k)+(r+s2/2)T/sÖT)
|
- |
e-rT k F(ln(S0/k)+(r-s2/2)T/sÖT)
|
Implies
- Black Scholes assumes m = r: stock
earns risk free return!!!
- Black Scholes assumes r' = r: discount at risk free rate!!!
Interpretation
- Option Interpretation: Call option price is independent of
expected appreciation (depreciation) of particular stock during contract period
- Insurance Interpretation: Agg stop price is independent of expected losses;
only volatility matters
- All cash flow discounted as though they are risk free
How can this be?
Risk in finance is an element of stochastic behavior
in future prices
- In GBM it is the term sZÖDt, creates "wiggles"
- Risk Free: locally deterministic price, like bank CD or bill in fixed interest
rate environment
Return above risk free rate required when future value
contains element of risk
- Each source of uncertainty commands a price, called market
price of risk
- Different stocks, oil futures, insurance derivatives
KEY POINT: Between underlying stock, bond and option there
is only one source of stochastic behaviour (uncertainty)
- Option and stock prices are instantaneously perfectly correlated
- Plausible: stock price and call price must move together
- Portfolio mixing the two in the right
proportions would be risk free
- Right proportion is dC/dS =: d < 1, hence "delta" hedging
- Law of one price implies gives option price
Basis of Option Pricing Paradigm
- Write an option and combine with portfolio of stocks and
bonds to remove all risk (wiggles)
- Cost of option = cost of setting up initial portfolio of stocks and bonds
provided no more cash flows required from trading
- Black Scholes paradigm shows price does equal cost of hedging portfolio
- Hence Black Scholes is a complete pricing paradigm
- Hedging portfolio "manufactures" option
- Option Pricing Paradigm does not rely on the law
of large numbers
- Obviously horrendous correlations exist in
portfolio of equities and options!
- Cost of initial portfolio independent of m, expected
return on stock
- Leads to notion of risk neutral valuation: can assume any convenient risk
preferences
- Risk neutral assumption: stocks earn risk free return hence m
= r
- Risk free portfolios earn the risk free return, hence r = r'
- Classic example of binary stock price model and explicit
hedging strategy is given in discussion
Cox and Ross
Investor's preferences and demand conditions in general
enter the valuation problem only in so far as they determine the equilibrium
parameter values. No matter what preferences are, as long as they determine
the same relevant parameter values, they will also value the option identically.
In the Black-Scholes case ... the only relevant parameters for the pricing problem
are r and sigma. To solve [for the price], then, we need only find the equilibrium
solution ... in some world where preferences are given and consistent with the
specified parameter values; the solution obtained will then be preference free.
Approach hinges on existence of traded underlying security
- Does not exist with many insurance products
- Work around possible in some cases
- Two options on same underlying (whether traded or not) share
a single source of uncertainty
- Same arguments used in Black Scholes imply there must be
a relation between prices of options at different strikes and expirations
- Could possibly be used to get constraints on Cat Options
where there is a single source of uncertainty
Fine Print on No-Arbitrage
No-Arbitrage means "no free lunch"
- No-arbitrage implies assets with equivalent cash flows command
the same price
- Alternative risk and packaging of risks should not lower
price - unless there is less coverage
- A model with arbitrages is not viable as a model
of market prices
since
- Agents would immediately act to change
prices!
Financial markets allow long and short positions
- If combinations A and B are equivalent
but not equally priced, the over-priced combination would be shorted by investors
who would buy B with the proceeds to produce an arbitrage profit
A geometric Brownian motion stock price process allows arbitrage
possibilities
- Doubling strategy
- Restrictions on the amount borrowed or on short sales needed
- No arbitrage is a consequence of the model framework not an assumption
Questions and Answers
Appendix
Full Discussion
Formulae typeset using LaTeX and translated from TeX by TTH,
version 2.34. 